1,003
8
0
Trenger hjelp med krefter og avstivning på opphengskonstruksjon til hengekøye
14
0
Jeg skal henge opp en hengekøye på verandaen og trenger å forlenge rekkverket på den ene siden i høyden. Rekkverket er i betong, men dette kan jeg ikke skru i. Derfor må jeg lage en trekonstruksjon som kan henge på. Slik bildet viser så ønsker jeg å få innfestingen til hengekøyen lengst mulig vekk, for å få de to opphengspunktene så langt fra hverandre som mulig.
Hvordan virker kreftene på denne konstruksjonen, og hvordan stiver man den av på best mulig måte? Tegning A innbiller jeg meg at er mest solid mtp kreftene nedover, men samtidig virker tegning B logisk siden skråavstivningen er mer i samme retning som kreftene fra hengekøya. Mulig det beste er å ha avstivning på skrå begge veier, men da begynner det jo etterhvert å bli en ganske voldsom konstruksjon, så om det ikke er nødvendig så er jo det det beste.
Jeg har ikke skrevet på mål og dimensjoner på tegningen siden jeg er mest interessert i prinsippene rundt kreftene.
Hvordan virker kreftene på denne konstruksjonen, og hvordan stiver man den av på best mulig måte? Tegning A innbiller jeg meg at er mest solid mtp kreftene nedover, men samtidig virker tegning B logisk siden skråavstivningen er mer i samme retning som kreftene fra hengekøya. Mulig det beste er å ha avstivning på skrå begge veier, men da begynner det jo etterhvert å bli en ganske voldsom konstruksjon, så om det ikke er nødvendig så er jo det det beste.
Jeg har ikke skrevet på mål og dimensjoner på tegningen siden jeg er mest interessert i prinsippene rundt kreftene.
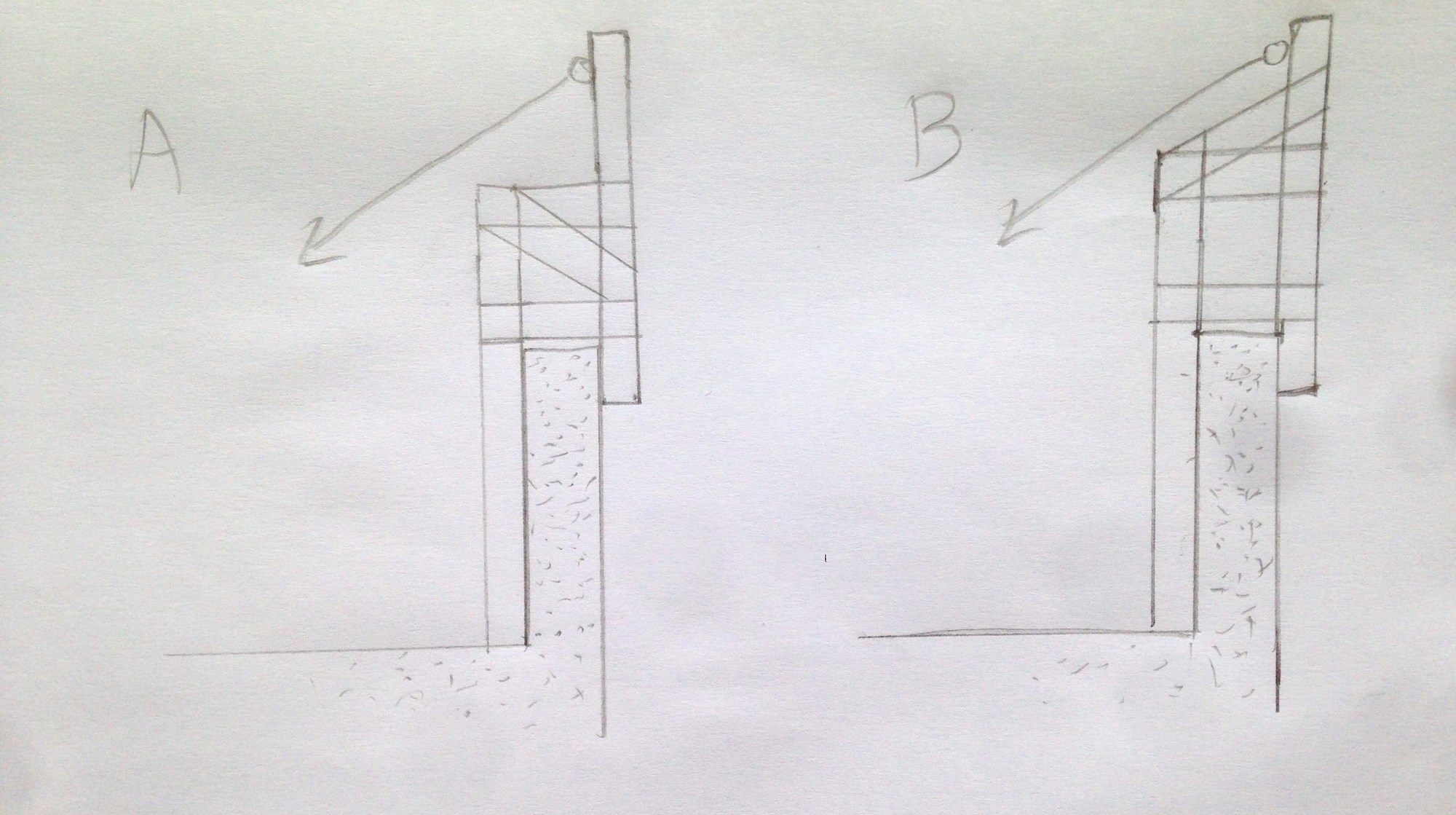
På B blir nevnte planke støttet opp av skråstiveren.
Dersom høyre vertikal er stiv nok, er det ingen forskjell på konstruksjonene.
En sak å tenke på er vinkelen ut fra selve festet og videre til hengekøya.
Litt vanskelig å forklare med ord, men figuren under beskriver dette greit:
http://klatreknerten.blogspot.no/2015/05/vinkel-og-kraft-i-topptaufestet.html
Hvorfor kan du ikke skru i betongen?
Spenner du en kjetting eller wire mellom en personbil og et tre og løfter på midten kan du lett trekke bilen opp av grøfta. Med tau er det vanskeligere da det strekker seg noe. Det hele er kraftkomponering fra ungdomsskolen.
Her vil slakk hengekøye være bedre en hardstrukket hengekøye mhp krefter i festet.
Regnet da med 300 kg belastning i hengekøya (det er maksbelastningen den er oppgitt for) og 64 grader (målt på midlertidig oppheng) mellom tau og festekonstruksjon.
Kan ikke skru i betongen siden alt utvendig tilhører borettslaget. Uansett kjedelig om man treffer på armering som får lyst til å ruste.
Hvis jeg forstår dette rett så har det ikke noe å si hvilken vei den skrå avstiveren står? Så forskjellen på A og B blir egentlig hvor godt støttet opp den øverste vertikale planken blir? Sett at jeg går for A, vil styrken på konstruksjonen øke med avstanden mellom de to parallelle vannrette avstiverne, eller vil det være optimalt at disse danner et kvadrat så den skrå avstiveren blir 45 grader?
Jeg ville helt klart ha gått for alternativ B. Høyre bjelke bør gå noe lenger ned langs muren.
Hvordan har du tenkt å sikre at dette ikke velter sidelengs?
Tenkte egentli først å bruke jekkestropp for å sikre sideveis, men laget et førsteutkast som ble for svakt, og da viste det seg at friksjonen man får pga belastningen gjør at alt står helt støtt.
Som KjellG skriver, det er fare for bøying av bjelken til høyre. Skråstaget vil redusere dette betraktelig.
Med A vil en få en bøyning mot venstre. Den øverste frie enden vil gi etter. Imidlertid, firkanten er ikke festet til rekkverket, bare hektet over. Det vil føre til at venste side i firkanten vil bøye seg noe og festet gli litt opp.
Med B vil toppen være stiv, men firkanten friere til å bøye seg.
Det stiveste blir å kombinere Aog B, men om det er nødvendig?